These are some notes I took while studying transformer models. I already implemented this paper on PyTorch.

Word Embeddings

Word embeddings are vector representations of words in a continuous, semantic space. Introduced with Word2Vec (Mikolov, 2013) [1301.3781], these embeddings encode the meaning of words as vectors, allowing relationships between words to be captured mathematically.

Unlike one-hot encoding, which only indicates the presence of a word and does not reflect meaning, word embeddings encode semantic content in a lower-dimensional space.

For example, vector arithmetic can capture analogies:

Word embeddings revolutionized transfer learning in NLP, improving feature extraction and enabling richer linguistic representations. The same concept has been extended to other domains, such as images, video, graphs, and audio, where models convert complex data into vectors containing relevant features.

Introduction to Traditional Recurrent Models

For a complete, working implementation of these models, feel free to explore the repository.

Before diving into the Transformer architecture, it’s important to understand traditional sequential models that have been widely used for sequence processing: Recurrent Neural Networks (RNN), Long Short-Term Memory (LSTM), and Gated Recurrent Units (GRU).

These models process input sequences step-by-step, maintaining a hidden state that captures previous information to influence how new inputs are interpreted.

class SequentialManyToOne(SequentialModel):
    """Sequential Model N to 1"""

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        batch, seq_len, _ = x.shape
        h = torch.zeros(batch, self.h_dim)
        c = torch.zeros(batch, self.h_dim) if self.seq_block.uses_c else None

        for t in range(seq_len):
            if self.seq_block.uses_c:
                h, c = self.seq_block(x[:, t, :], h, c)
            else:
                h = self.seq_block(x[:, t, :], h)
        out = self.out_layer(h)
        return out

• RNN (Simple Recurrent Neural Network):

  Updates the hidden state by applying a nonlinear function to the combination of the current input and the previous hidden state. However, RNNs struggle to capture long-term dependencies due to vanishing gradients.

class RNNBlock(SequentialBlock):
    def forward(self, x: torch.Tensor, h_prev: torch.Tensor) -> torch.Tensor:
        h = self.act_fn(self.w(x) + self.u(h_prev))
        return h

• LSTM (Long Short-Term Memory):

  Introduces gates (forget, input, output) to regulate the flow of information, allowing the network to remember or forget information over long sequences. It maintains both a hidden state and a separate cell state. While LSTMs alleviate the vanishing gradient problem, they may still suffer from exploding gradients in certain situations.

class LSTMBlock(SequentialBlock):
    def forward(
        self, x_t: torch.Tensor, h_prev: torch.Tensor, c_prev: torch.Tensor
    ) -> tuple[torch.Tensor, torch.Tensor]:
        f_t = self.sigmoid(self.w_f(x_t) + self.u_f(h_prev))
        i_t = self.sigmoid(self.w_i(x_t) + self.u_i(h_prev))
        o_t = self.sigmoid(self.w_o(x_t) + self.u_o(h_prev))
        c_t_candidate = self.tanh(self.w_c(x_t) + self.u_c(h_prev))

        c_t = f_t * c_prev + i_t * c_t_candidate
        h_t = o_t * self.tanh(c_t)

        return h_t, c_t

• GRU (Gated Recurrent Unit):

  A simpler alternative to LSTM that uses only two gates: update and reset gates to control the hidden state, achieving competitive performance with fewer parameters.

class GRUBlock(SequentialBlock):
    def forward(self, x_t: torch.Tensor, h_prev: torch.Tensor) -> torch.Tensor:
        z_t = self.sigmoid(self.w_z(x_t) + self.u_z(h_prev))
        r_t = self.sigmoid(self.w_r(x_t) + self.u_r(h_prev))
        h_t_candidate = self.tanh(self.w_h(x_t) + self.u_h(r_t * h_prev))
        h_t = (1 - z_t) * h_prev + z_t * h_t_candidate
        return h_t

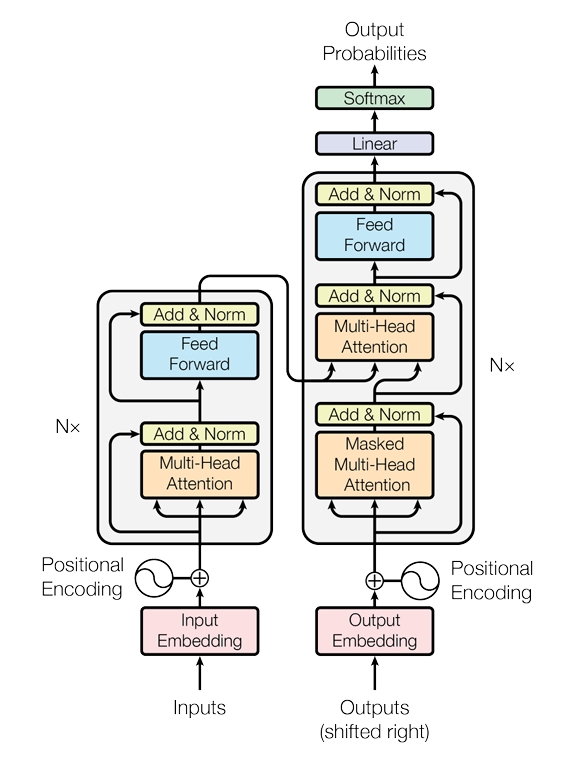
Transformer Architecture

First of all we are going to introduce all different layers used in transformers paper.

Attention

Word embeddings [1301.3781] provided a significant improvement to language models by allowing the semantic content of a word to be represented in a linear space.

One of the main issues with word embeddings is that they do not take into account for the context of words within a sentence. The same word can have different meanings depending on its context (polysemy), its representation in word embeddings remains the same regardless of where it appears. Additionally, if a word is unknown to the word embedding model or is misspelled, its representation becomes inefficient or useless.

This is why the Transformers paper introduces attention, which consists of a new embedding layer designed to capture the context of a word. In this way, attention will be represented as a \(T \times T\) matrix containing the relationship of each word with the rest of the text, and the contextual embedding is an embedding that not only takes into account the word embeddings but also includes information from the other words through attention. Represented as a \(T \times d_v\) matrix.

This is illustrated in the following image, every word in sentence is related with the rest of words:

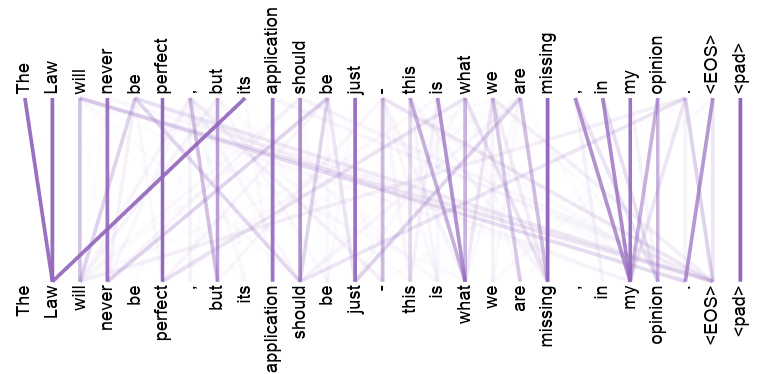
Scaled Dot-Product Attention

The Scaled Dot-Product Attention computes a weighted sum of value vectors, where the weights are determined by the compatibility between queries and keys.

To obtain attention, the query (Q) is the question a token asks the rest of the text: “What information do I need, and from whom?”. The key (K) describes the type of information a token holds and can offer to others. The value (V) contains the actual information that will be shared if the key of a token matches the query of another. In other words, while the query-key interaction determines which tokens are relevant to each other (attention), the value is the payload of that interaction, the contextual content that will be passed along and integrated into the representation of the querying token.

Given the input \(X \in \mathbb{R}^{B \times T \times d_{model}}\), we project it into the query, key, and value spaces:

We then compute the attention scores via the dot product between each query and keys:

Finally, the context vectors are obtained by a weighted sum of the values:

Notation:

• \(B\) batch size
• \(T\) sequence length
• \(d_{model}\) embedding length
• \(d_k\) query dimension
• \(d_v\) value dimension

class AttentionLayer(nn.Module):
    """Scaled Dot-Product Attention"""

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        query = self.q_layer(x)
        key = self.k_layer(x)
        value = self.v_layer(x)

        attention = self.softmax(
            (query @ key.transpose(-2, -1)) / self.d_k_sqrt
        )
        context = attention @ value
        return context

Attention Masking

To train an encoder, it is beneficial for the attention modules to have context of the entire sentence so they can learn the relationships that words should have.

In contrast, when dealing with decoders, it is better not to have context of future words, as that would be “cheating.” To prevent this, attention masking is used, which ensures that, for example, the third word only considers the first three words and ignores the subsequent ones.

Mathematically, it is defined as:

Since we apply softmax, the upper triangle of the attention matrix (all future values for a token) has a value of 0.

class AttentionLayer(nn.Module):
    """Scaled Dot-Product Attention masked"""

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        query = self.w_q(x)
        key = self.w_k(x)
        value = self.w_v(x)

        attention = (query @ key.transpose(-2, -1)) / self.d_k_sqrt
        if self.masking:
            seq_len = attention.size(-1)
            mask = torch.triu(torch.ones(seq_len, seq_len, device=attention.device), diagonal=1)
            attention = attention.masked_fill(mask.bool(), float('-inf'))

        score = self.softmax(attention)
        context = score @ value
        return context

Multi-Head Attention

The Transformer paper introduced multi-head attention: instead of computing a single attention, we compute attention across \(h\) heads, concatenate the results, and apply a linear projection:

Where \(W_i^Q,\space W_i^K \in \mathbb{R}^{d_{model} \times dk};\quad W_i^V \in \mathbb{R}^{d_{model} \times d_v};\quad W^O \in \mathbb{R}^{hd_v \times d_{model}}\).

class MultiHeadAttention(nn.Module):
    """MultiHead Attention"""

    w_heads = nn.ModuleList([
        AttentionLayer(d_model, self.d_k, self.d_v)
        for _ in range(h)
    ])
    
    def forward(self, x: torch.Tensor) -> torch.Tensor:
        heads = [head(x) for head in self.w_heads]
        x_head = torch.cat(heads, dim=-1)
        context = self.w_o(x_head)
        return context

Add & Norm Layer

It’s a very simple layer but is used constantly in Transformer-like models. It consists of combining two inputs (of the same shape) via summation and then applying normalization.

The purpose of applying normalization to the output is to prevent gradients from vanishing or exploding.

class AddAndNorm(nn.Module):
    """Add & Norm Layer"""
    
    def forward(self, x: torch.Tensor, y: torch.Tensor) -> torch.Tensor:
            return self.norm(x + y)

Position-wise Feed-Forward Networks

This type of layer works like an encoder-decoder but in the opposite direction: it takes an input of one dimension, applies a network to expand it to a larger dimension, and then applies another linear network to reduce it back to the original dimension.

According to literature, FFNs could be considered as two convolutions with kernel size 1.

Mathematically:

class PositionWiseFFN(nn.Module):
    """Position-wise Feed-Forward Networks, works as two convolutions with kernel size 1."""

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        y1 = self.relu(self.fc1(x))
        y2 = self.fc2(y1)
        return y2

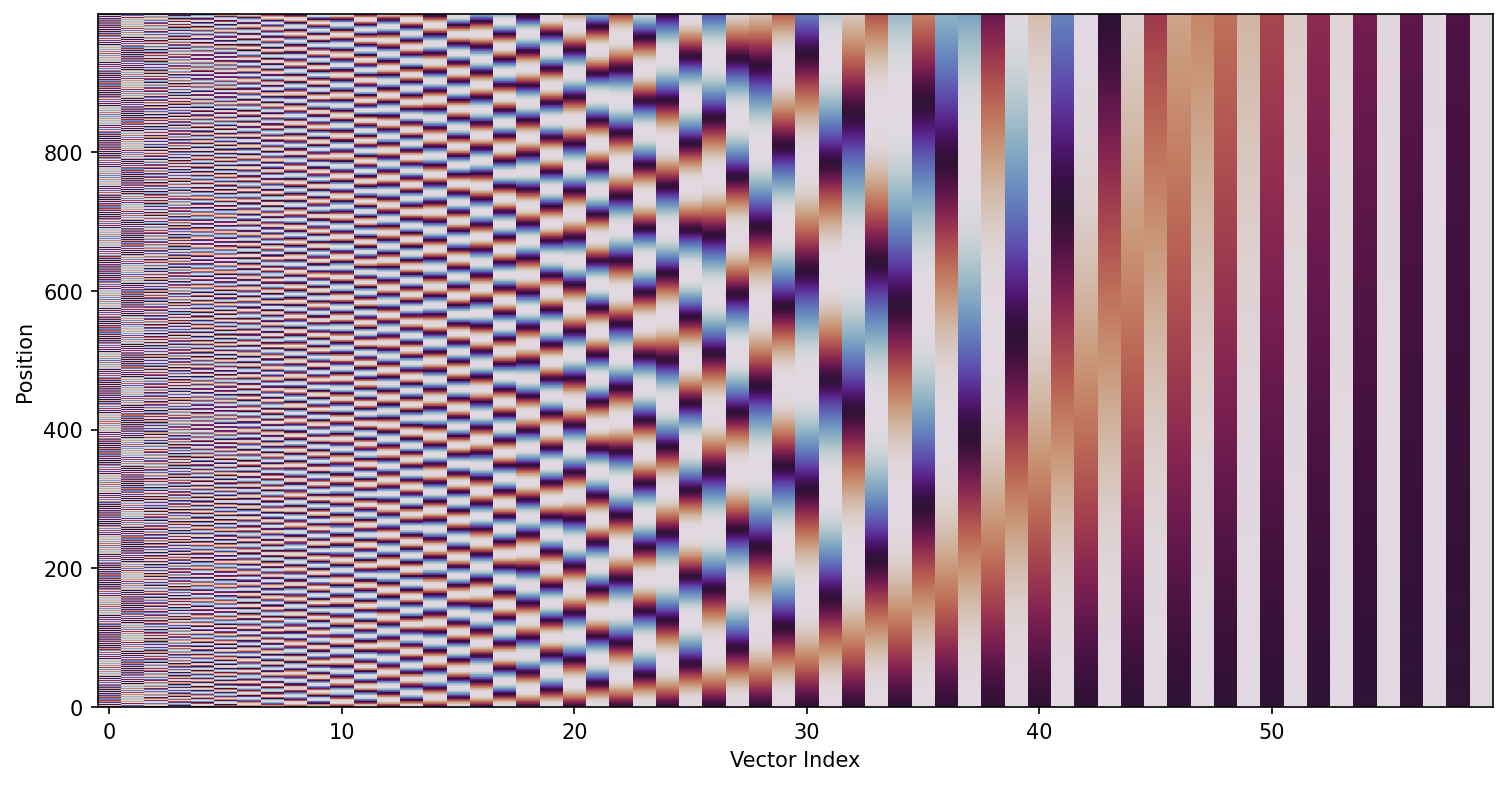
Positional Encoding

Since transformer models use attention and not recurrence or convolution, there is no way for the model to capture the positional context of words and their order. Positional information is injected into the model for this purpose, using positional encodings.

Transformers use Sinusoidal Positional Encodings:

Each dimension of the positional encoding corresponds to a sinusoid.

All values of \(pos\) between 0 and 10000⋅2π produce positional encodings that are practically linearly independent. For larger positions, the sinusoidal patterns may start to repeat due to their periodic nature, potentially reducing the model’s ability to distinguish positions uniquely.

Transformer Encoder

Transformer encoders consist of the concatenation of N blocks:

class Encoder(nn.Module):
    """Transformer's Encoder Model"""

    def forward(self, in_emb: torch.Tensor, pos_emb: torch.Tensor) -> torch.Tensor:
        x = in_emb + pos_emb
        for encoder_layer in self.encoder_layers:
            x = encoder_layer(x)
        return x

Where each encoder layer:

class EncoderLayer(nn.Module):
    """Transformer's Encoder Layer"""

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        att_out = self.multi_head_attention(x)
        x = self.add_norm_1(x, att_out)

        ff_out = self.feed_forward(x)
        x = self.add_norm_2(x, ff_out)
        return x